Notebook
对抗样本生成算法
论文阅读
- EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES(FGSM)
- Reliable Evaluation of Adversarial Robustness with an Ensemble of Diverse Parameter-free Attacks(APGD)
FGSM
对抗样本的基本原理 \(\omega^T x'=\omega^T x+\omega^T \eta\)
fast gradient sign method 用于生成对抗样本。
\[\eta=\epsilon sign(\nabla_x J(\theta,x,y))\]对抗训练
\[J'(\theta,x,y)=\alpha J(\theta,x,y)+(1-\alpha)J(\theta,x+\epsilon sign(\nabla_x J(\theta,x,y)),y)\]对于对抗样本泛用性的解释
 对抗样本的一个有趣方面是,为一个模型生成的示例经常被其他模型错误分类,即使它们具有不同的架构或在不相交的训练集上进行了训练也是如此。此外,当这些不同的模型对一个对抗样本进行错误分类时,它们通常在类别上彼此一致。基于极端非线性和过度拟合的解释不能轻易地解释这种现象-为什么具有过多容量的多个极端非线性模型必须以相同的方式一致地标记分布点?从以下假设来看,这种行为尤其令人惊讶:对抗样本像现实中的有理数一样精细地平铺空间,因为在这种观点中,对抗样本很常见,但仅在非常精确的位置发生。
对抗样本的一个有趣方面是,为一个模型生成的示例经常被其他模型错误分类,即使它们具有不同的架构或在不相交的训练集上进行了训练也是如此。此外,当这些不同的模型对一个对抗样本进行错误分类时,它们通常在类别上彼此一致。基于极端非线性和过度拟合的解释不能轻易地解释这种现象-为什么具有过多容量的多个极端非线性模型必须以相同的方式一致地标记分布点?从以下假设来看,这种行为尤其令人惊讶:对抗样本像现实中的有理数一样精细地平铺空间,因为在这种观点中,对抗样本很常见,但仅在非常精确的位置发生。
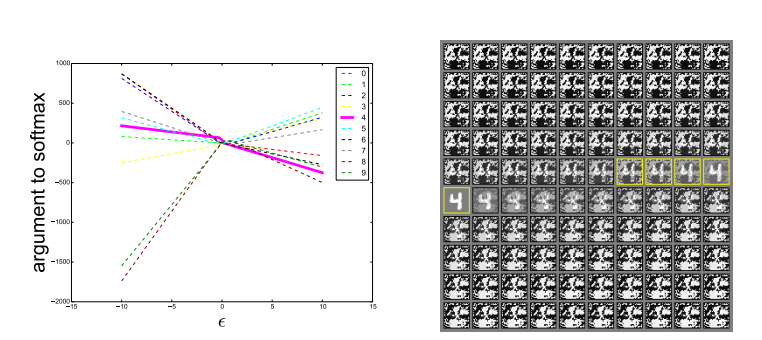
在线性视图下,对抗样本出现在较宽的子空间中。方向 $\eta$ 仅需要具有成本函数梯度的正点积,而 $\epsilon$ 只需足够大即可。下图展示了这种现象。通过找出 $\epsilon$ 的不同值,我们可以看到对抗样本出现在由快速梯度符号方法定义的1-D子空间的连续区域中,而不是在细小口袋中。这就解释了为什么对抗样本很多,以及为什么一个分类器错误分类的示例具有较高的先验概率被另一个分类器错误分类的原因。
参考文献
FGSM
FGSM的快速在于它不需要迭代过程即可计算对抗样本,因此比其他考虑的方法要快得多。
\[X^{adv}=X+\epsilon sign(\nabla_x J(X,y_{true}))\]BIM
\[X^{adv}_0 =X\\ X^{adv}_{N+1}=Clip_{X,\epsilon}\{X^{adv}_{N}+\alpha sign(\nabla_x J(X^{adv}_{N},y_{true}))\}\](其中 $Clip_{X,\epsilon}{X’}=\min(\max(X’,X-\epsilon),X+\epsilon) $ )
在 BIM中,每次迭代都会向原始输入添加一个小的扰动,该扰动是基于当前对抗性样本的梯度方向和步长参数计算得到的。由于每次迭代都只添加了一个小的扰动,经过多次迭代后,Clip函数能保证总的扰动强度通常不会超过预先设定的最大扰动限制 $\epsilon$。
这种限制确保了对抗性样本在一定程度上仍然保持与原始输入的相似性,同时具有足够的扰动来欺骗分类器。通过逐渐增加扰动,BIM 能够生成具有更高欺骗性的对抗性样本,同时保持了一定的约束,以防止扰动过大而影响样本的真实性质。这种权衡可以根据特定应用的需求和安全性要求进行调整。
ILCM
Alexey Kurakin,Ian J. Goodfello,Samy Bengio “ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD”,ICLR,2017
目前为止的两种方法,都只是试图增加正确类的损失,而没有指定模型应该选择哪个错误类。我们引入了Iterative Least-likely Class Method(最不可能的类方法)。这种迭代方法尝试制作一个对抗图像,将其分类为特定的所需目标类别。
对于期望的类别,我们根据图像上训练网络的预测选择了可能性最小的类别:
\[y_{LL}=\arg\min_{y}\{p(y|X)\}\]为了最大化 $\log p(y_{LL}\vert X)$ ,我们在 $sign{\nabla_{X} \log(p(y_{LL}\vert X))}$ (对于交叉熵损失的神经网络,其等于 $sign{-\nabla_{X}J(x,y_{LL})}$)方向上进行迭代. 故有以下过程we
\[X^{adv}_0 =X\\ X^{adv}_{N+1}=Clip_{X,\epsilon}\{X^{adv}_{N}-\alpha sign(\nabla_x J(X^{adv}_{N},y_{LL}))\}\]PGD
\(X^{adv}_0 =X\\ X^{adv}_{N+1}=\prod_{X+S}\{X^{adv}_{N}+\alpha sign(\nabla_x J(X^{adv}_{N},y_{true}))\}\)
这个算法和BIM基本是相同的,可以理解为BIM的推广,主要区别在于对原始样本有一个加入随机噪声的操作
Does PGD not need to perform random restart in every iterative ? Is it enough to start with random noise at FGSM? https://github.com/MadryLab/mnist_challenge/issues/3
JSMA
初始化:给定原始样本 $x$ 和目标标签 $t$,设置迭代次数 $T$ 和扰动大小约束 $\epsilon$。
迭代更新:进行 $T$ 次迭代,每次更新对抗样本 $x_{\text{adv}}$:
- 计算模型的输出关于输入 $x_{\text{adv}}$ 的Jacobian矩阵 $\frac{\partial f(x_{\text{adv}})}{\partial x_{\text{adv}}}$,其中 $f(x_{\text{adv}})$ 是模型的输出。
- 计算每个特征 $i$ 对目标标签 $t$ 的相对重要性(saliency score): \(S_i = \frac{\partial f_t(x_{\text{adv}})}{\partial x_{\text{adv},i}} \cdot \left| \frac{x_{\text{adv},i} - x_i}{x_{\text{adv},i}} \right|\)
- 选择相对重要性最高的特征,即 $i^* = \arg \max_i S_i$。
投影操作:在每个迭代步骤之后,对对抗样本 $x_{\text{adv}}$ 进行投影,以确保其在合理范围内: \(x_{\text{adv}} = \text{clip}(x_{\text{adv}}, x - \epsilon, x + \epsilon)\)
选择相对重要性最高的特征是为了最大化对抗样本的影响,从而降低模型的准确性。通过迭代的方式,在每个步骤中选择和扰动特征,JSMA算法可以逐渐改变对抗样本,以在尽可能小的扰动下实现误分类。
CW(Carlini and Wagner Attack)(TODO)
Towards Evaluating the Robustness of Neural Networks
CW算法的目标是在给定输入样本 $x$ 和目标标签 $t$ 的情况下,找到一个扰动 $\delta$,使得模型输出 $f(x + \delta)$ 与目标标签 $t$ 之间的损失最小化。CW算法最小化的损失函数如下:
\[J(\delta) = \text{dist} + c \cdot \text{loss}(f(x + \delta), t)\]其中,$\text{dist}$ 衡量扰动的大小(可以是L1、L2或L $\infty$ 范数),$c$ 是一个权衡系数,$\text{loss}$ 是用来衡量模型误分类程度的损失函数。
优化过程:CW算法通过解决上述损失函数的优化问题,找到最小的扰动 $\delta$,使得模型的输出接近目标标签 $t$ 。优化过程通常使用优化方法,如L-BFGS(Limited-memory Broyden-Fletcher-Goldfarb-Shanno)。
MIM(Momentum Iterative Method)
Boosting Adversarial Attacks with Momentum \(g_{t+1}=\mu*g_{t}+\frac{\nabla_x J(X,y_{true})}{\|\nabla_x J(X,y_{true})\|}\\ x^{adv}_{t+1}=x^{adv}_{t}+\alpha*sign(g_{t+1})\)
在BIM的基础上增加动量
几个基本算法的比较
| 算法 | 准确率 | 扰动 |
|---|---|---|
| 随机扰动 | 97% |  |
| FGSM | 88% |  |
| PGD | 85% | 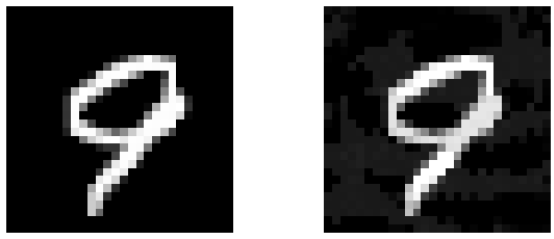 |
| MIM | 85% |  |
| APGD(参数逐渐降低) | 84% |  |
这里实际上不同算法使用的参数大小是不一样的
对抗攻击的12种攻击方法和15种防御方法
One Pixel Attack:极端的对抗攻击方法,仅改变图像中的一个像素值就可以实现对抗攻击。
DeepFool: 通过迭代计算的方法生成最小规范对抗扰动,将位于分类边界内的图像逐步推到边界外,直到出现错误分类。作者证明他们生成的扰动比 FGSM 更小,同时有相似的欺骗率。
Universal Adversarial Perturbations: 使用的方法和 DeepFool 相似,都是用对抗扰动将图像推出分类边界,不过同一个扰动针对的是所有的图像。
对抗训练的作用
对抗训练前:
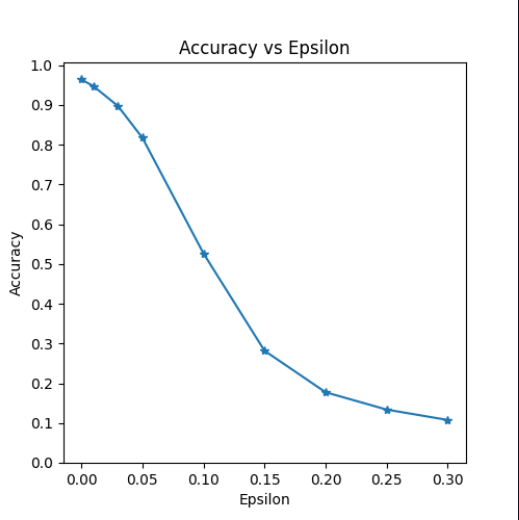
对抗训练后: